Οι ασκήσεις αυτές αξιοποιούν την έννοια του κλάσματος σε περιβάλλον σπαζοκεφαλιάς και προσφέρονται για την εξάσκηση σε πράξεις κλασμάτων.
φυλλάδιο
φυλλάδιο
 Τέσσερα προβλήματα αναγωγής στην κλασματική μονάδα. Η δυσκολία τους έγκειται στην ανάγκη κατανόησης της έννοιας του κλάσματος, αφού κάθε φορά οι μαθητές θα πρέπει να επιλέγουν αν θα διαιρέσουν με τον αριθμητή ή με τον παρονομαστή.
Τέσσερα προβλήματα αναγωγής στην κλασματική μονάδα. Η δυσκολία τους έγκειται στην ανάγκη κατανόησης της έννοιας του κλάσματος, αφού κάθε φορά οι μαθητές θα πρέπει να επιλέγουν αν θα διαιρέσουν με τον αριθμητή ή με τον παρονομαστή. Ο σύνδεσμος που ακολουθεί παραπέμπει σε μία από τις άπειρες ηλεκτρονικές εφαρμογές που μπορεί να φανεί χρήσιμη σε δασκάλες και δασκάλους που διαθέτουν διαδραστικό πίνακα (ή υπολογιστή και προτζέκτορα) και σύνδεση με το διαδίκτυο στην τάξη τους. Κάνει λίγο πιο εύκολη τη διδασκαλία της έννοιας του κλάσματος και τις συγκρίσεις κλασμάτων. Κερδίζεις χρόνο κι έτσι διευκολύνεις την μετατροπή των εννοιών σε εικόνες. Ίσως όμως χάνεις σε σκέψη και φαντασία. Μάλλον θα ήταν προτιμότερο να χρησιμοποιείται με μέτρο. https://www.mathlearningcenter.org/web-apps/fractions/
Ο σύνδεσμος που ακολουθεί παραπέμπει σε μία από τις άπειρες ηλεκτρονικές εφαρμογές που μπορεί να φανεί χρήσιμη σε δασκάλες και δασκάλους που διαθέτουν διαδραστικό πίνακα (ή υπολογιστή και προτζέκτορα) και σύνδεση με το διαδίκτυο στην τάξη τους. Κάνει λίγο πιο εύκολη τη διδασκαλία της έννοιας του κλάσματος και τις συγκρίσεις κλασμάτων. Κερδίζεις χρόνο κι έτσι διευκολύνεις την μετατροπή των εννοιών σε εικόνες. Ίσως όμως χάνεις σε σκέψη και φαντασία. Μάλλον θα ήταν προτιμότερο να χρησιμοποιείται με μέτρο. https://www.mathlearningcenter.org/web-apps/fractions/

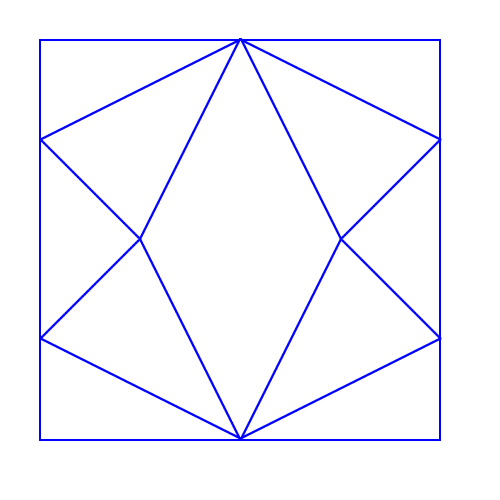 |
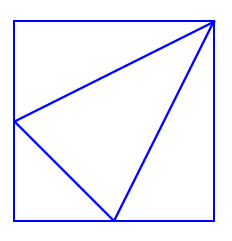
| πηγή: https://nrich.maths.org/ |

 |
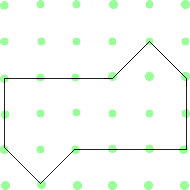
| πηγή https://nrich.maths.org/2086 |
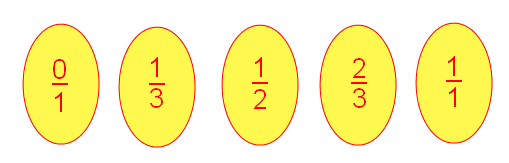

 Στις ασκήσεις αυτές οι μαθητές συμπληρώνουν τον αριθμητή ή τον παρονομαστή που λείπει, έτσι ώστε να ισχύει η αυτοδυναμία δύο κλασμάτων. φυλλάδιο
Στις ασκήσεις αυτές οι μαθητές συμπληρώνουν τον αριθμητή ή τον παρονομαστή που λείπει, έτσι ώστε να ισχύει η αυτοδυναμία δύο κλασμάτων. φυλλάδιο  Στις ασκήσεις αυτές οι μαθητές προσθέτουν μεικτούς αριθμούς με ομώνυμα κλάσματα. Οι ασκήσεις συνοδεύονται από εικόνες που βοηθούν στην κατανόηση του αλγόριθμου.
Στις ασκήσεις αυτές οι μαθητές προσθέτουν μεικτούς αριθμούς με ομώνυμα κλάσματα. Οι ασκήσεις συνοδεύονται από εικόνες που βοηθούν στην κατανόηση του αλγόριθμου. |
| πηγή: Common Core Sheets |